

#How to make an equation in word how to#
How to type chemical equation and arrows in Word 2007 and above.įor older versions of MS Word, go to the insert menu and click on the equation, which launches the Equation Editor Program (you can also find this program on your computer by searching for eqnedt.exe), which gives you the same ability to create equations. Note: Get creative with math by turning a mathematical equation into a story. If you need to type above or below arrow just type "\above(text above arrow goes here)".Similarly tying below arrow just type \below(test below goes here)". For up arrow and down arrow showing gas liberation and precipitation use \uparrow or \downarrow followed by space Shortcut for typing arrows of chemical equation in Word 2007 and above.Ĭlick on the word "yields" and replace it with as many spaces as you need to create an arrow of whatever length you want. To get a long arrow, click on the operator but and choose the arrow with the word "yields" written over it under common operator structures. This feature on Word will also accept some (but not all) tex commands for formatting equations. You have access to a wide range of arrows from a pull-down menu, but -> will give you a simple right arrow (although it is not very long). Additionally, people can copy and paste equations from other programs. With Word, users can quickly insert existing equations, add specific formulas and save them for future use, or draw them with the mouse or touch. For example, underscore _ creates a subscript and a caret ^ creates a superscript Shortcut for typing subscript and superscript in MS Word 2007|2010|2013|2016 and office 365. Fortunately, Microsoft Office offers a number of tools that make life a little easier to enter math formulas.
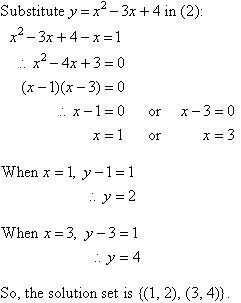
There are also shortcut commands to render most the common things you want. The default is to have letters italicized (as variables), so you will want to fix that. Alternatively you can use _ for subscript and ^ for superscript. Use the buttons in the ribbon to do superscripts and subscripts. (For shortcut you can press Alt+= sight together)Ĭlick on the equation button on the far right. It is designed for math but works okay for chemistry. Then in the last step (answering the question that was asked), we’d have to evaluate ?y+7? (to get John’s age seven years from now), and our answer would be ?32+7=39?.If you are using MS Word 2007 or newer, use the equation feature. To solve this problem, it would be convenient to define ?x? as Mary’s age now, and ?y? as John’s age now, because we’re given a relationship between Mary’s age (now) and John’s age (now). If Mary is now ?18?, how old will John be seven years from now? Suppose we’d been given the following word problem instead:Ĭurrently, John’s age is four less than twice Mary’s age. Since we defined ?y? as John’s age, the answer is ?32?. The final step is to answer the question that was asked. Here, we’re given Mary’s age as ?18?, so we substitute ?18? for ?x? and then solve for ?y?. The third step in solving a word problem is to use the given data and solve the equation. To see this, it may help to think of the word “is” as having the same meaning (in math) as “is equal to.”Ĭombining all of these, we get the equation How about the word “is” (in “John’s age is four less than twice Mary’s age”)? Well, “is” is translated as an equals sign. Here, “John’s age” is translated as “?2x-4?.” The next step in solving a word problem is to “translate” each word or phrase into mathematical symbols. So we’ll define the variables by saying “Let ?x? be Mary’s age, and let ?y? be John’s age.” (We could use any letters of the alphabet for the variables, but people often use ?x? for one of the variables, and if there are one or two additional variables, they tend to use ?y? and ?z?, in that order.) In this problem, we have two quantities: Mary’s age and John’s age. What that means is to state the particular quantity that each variable stands for. The first step in solving a word problem like this is to define the variables. John’s age is four less than twice Mary’s age. Not only can we translate phrases into expressions, but we can write equations from some phrases as well.įor instance, suppose you wanted to use algebra to solve the following word problem:


 0 kommentar(er)
0 kommentar(er)
